Tra i più semplici modelli di apprendimento supervisionati c’è quello basato sulla regressione lineare. Il funzionamento di una semplice regressione lineare è alla base di molto più complessi come le reti neurali artificiali.
In poche parole quello che fa la regressione lineare e stabilire una correlazione tra una variabile dipendente y ed una variabile indipendente x sotto forma di un polinomio di primo grado con tanti termini quante sono le figure del nostro dataset:
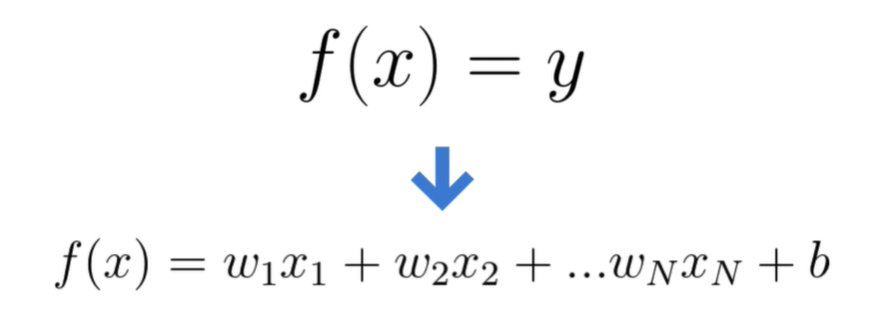
Facciamo un semplice esempio: immaginiamo di avere una dataset dove una serie di appartamenti caratterizzati da due variabili quantitative continue come ad esempio il valore in euro e la grandezza in metri quadri. Immaginiamo di voler costruire un modello capace di predire il valore di un appartamento in base alla sua grandezza in metri quadri.
| METRI QUADRI | VALORE € |
|---|---|
| 100 | 145.000 |
| 120 | 180.000 |
| 60 | 110.000 | 130 | 200.000 | 80 | 140.000 | 190 | 220.000 | 200 | 250.000 | 140 | ??? |
Un problema di regressione lineare si può ridurre ad individuare la relazione che ci permette di tracciare la funzione f(x) che ad ogni valore di x (variabile indipendente) ci permette di individuare il valore y del nostro target (variabile dipendente), ovvero nel nostro caso ci permette di conoscere il valore di un appartamento partendo dalla sua grandezza in metri quadri.
Considerando il problema da un punto di vista grafico possiamo tracciare in uno scatter plot i vari punti dei nostri appartamenti ponendo nell’asse delle ascisse la grandezza in metri quadri e nell’asse delle ordinate il valore in euro. In questo esempio si rileva che ad un amento dei metri quadri corrisponderà un aumento del valore dell’immobile e possiamo esprimere questa relazione grazie ad una retta di regressione.
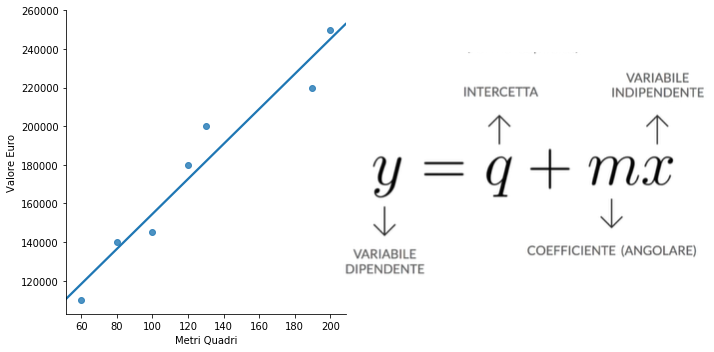
La regressione consiste nel tracciare la retta che più si avvicina a tutti i punti del grafico, stabilendo in questo modo una relazione tra la variabile indipendente e quella dipendente. Una retta può essere scritta come una equazione in maniera esplicita dove di y risulta essere il la somma tra il valore q (intercetta della retta con l’asse Y) ed il prodotto della variabile indipendente x con m (il coefficiente angolare che determina l’inclinazione della retta).
I valori q ed m sono quello che la regressione lineare deve ottimizzare per trovare la retta che meglio si adatta i punti del nostro grafico. Nel piano cartesiano possono essere rappresentate rette, per trovare in valori di q ed m che meglio esprimono la relazione tra valore dell’immobile e metri quadri dobbiamo utilizzare una funzione di costo.
La funzione di costo
Una funzione di costo fornisce una distanza tra il nostro modello e quello ideale, ovvero il modello che ritorna sempre il risultato corretto. Serve quindi per confrontare un modello di machine learning con quello idealmente perfetto.
Esistono diversi tipi di funzione di costo ma, per quanto riguarda la regressione lineare di cui abbiamo parlato nell’articolo precedente, la funzione di costo più utilizzata è quella della somma dei quadrati residui chiamata in inglese Sum of the Squared Residual (RRS).
Per calcolare la somma dei quadrati residui dobbiamo andare a calcolare per ogni elemento della nostra osservazione la differenza tra il valore reale ed il valore predetto dalla nostra regressione lineare elevandola al quadrato per poi sommare tutti i valori ottenuti
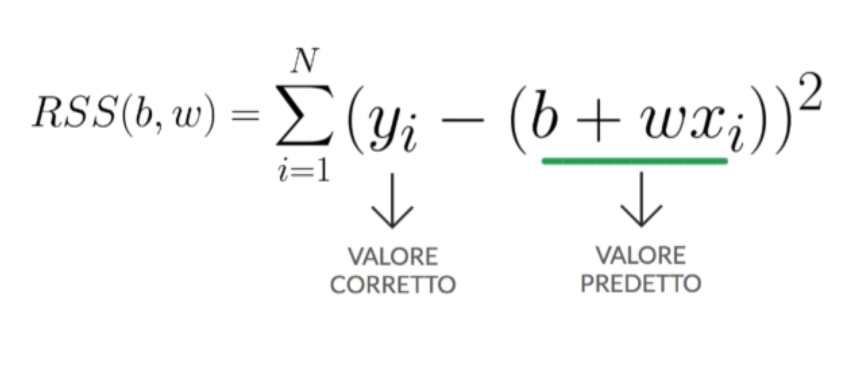
Minore è il risultato della funzione di costo e maggiore sarà la qualità del nostro modello, questa metrica ci permette di misurare quanto è valido un modello. A questo punto abbiamo bisogno di un metodo che ci permetta di minimizzare la nostra funzione di costo: per questo compito dobbiamo affidarci ad un algoritmo di ottimizzazione a cui dedicheremo il prossimo post..
