Nei casi più semplici un ottimizzatore ci permette di conoscere il massimo ed il minimo di una funzione: nello specifico quei parametri che passati alla funzione ci permettono di trovarne il suo valore massimo ed il suo valore minimo.
Nel caso di una o due variabili l’individuazione del punto minimo o massimo è abbastanza facile ed intuitiva anche solo guardando la rappresentazione grafica della nostra funzione in un piano a due o tre dimensioni. Ma quando il numero della variabili aumenta difficilmente possiamo concepire una soluzione per il nostro problema: ed è qui che entra in gioco il machine learning.
Gli algoritmi di ottimizzazione ci permettono di individuare i coefficienti ideali che passati alla funzione ci permettono di avvicinarci al più possibile ai valori reali con le nostre previsioni.
Esistono numerosi algoritmi di ottimizzazione con varie caratteristiche che li rendono più o meno adatti a determinati modelli di machine learning.
- Gradient Descendt
- ADAM
- Adadelta
- Adagrad
- Adamax
- RMSprop
- Stochastic Gradient Descendt
L’algoritmo di ottimizzazione più facile da comprendere ed al tempo stesso molto utilizzato è il Gradiend Descendt: che consiste nell’andare a stimare il punto di minimo della funzione di costo.
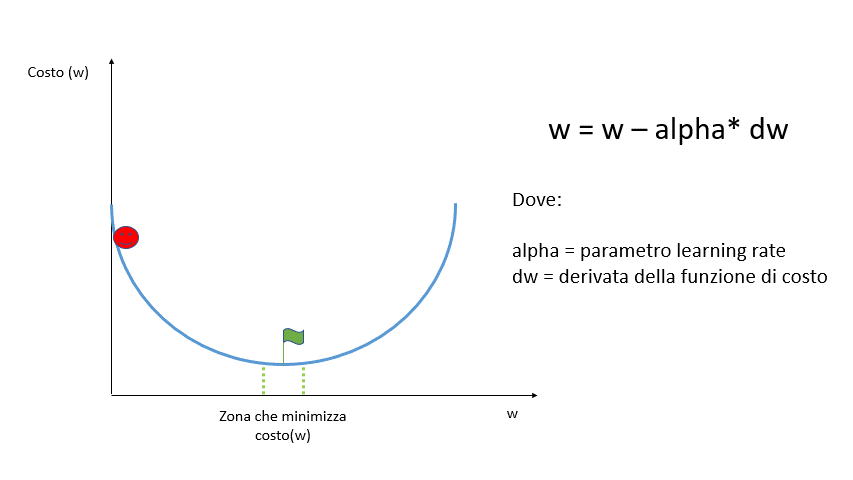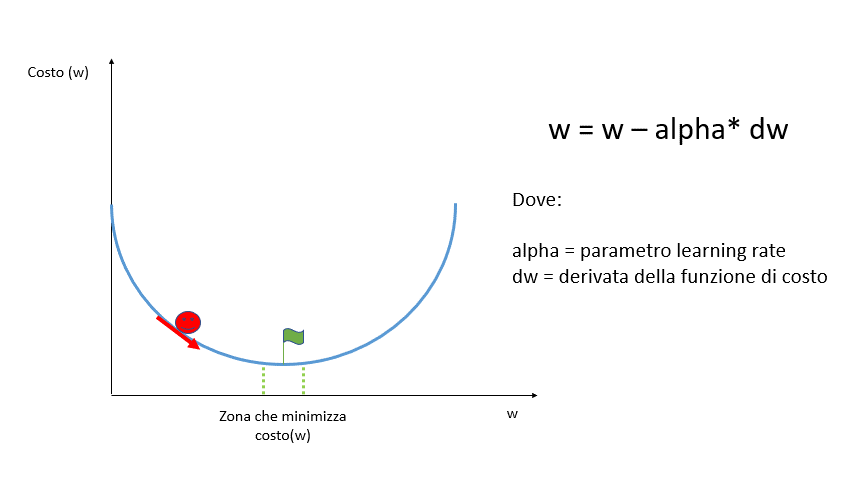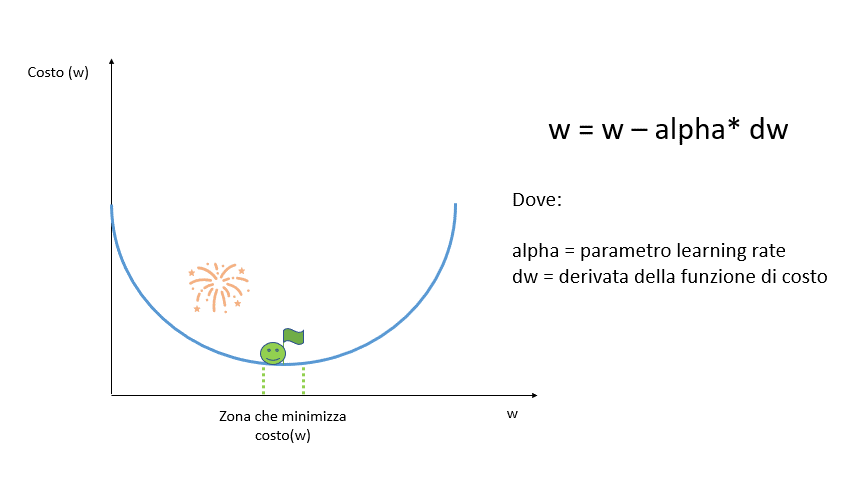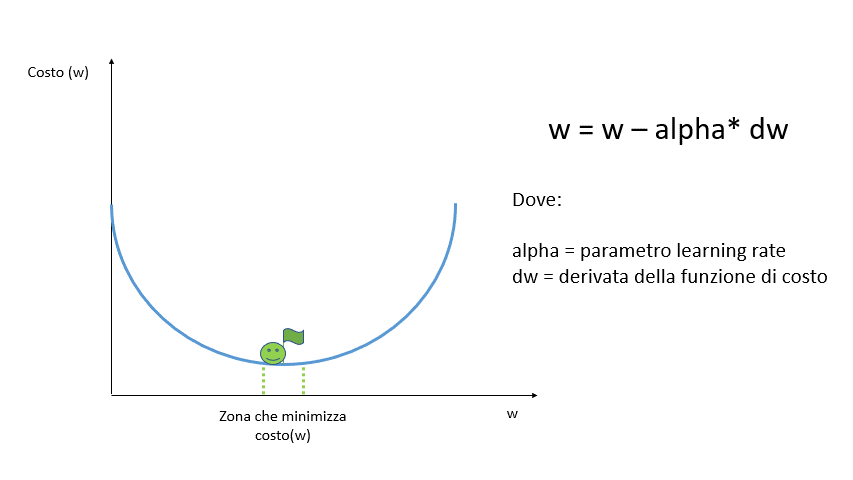
Partendo da un punto casuale si calcola la derivata della funzione di costo di quel punto per verificare l’inclinazione della curva alla ricerca del punto di minimo in cui la derivata dovrebbe essere pari a zero.
La derivata di una funzione è pari a zero se la funzione è costante, è negativa se la funzione è decrescente ed è positiva se è crescente.
Per muoverci lungo la funzione dobbiamo scegliere un valore arbitrario alpha chiamato learning rate che indica la velocità (o la grandezza dei passi) con cui dobbiamo spostarci.
Parametri troppo grandi di alpha ci faranno saltare da una parte all’altra della curva facendoci mancare il punto di minimo, mentre parametri troppo piccoli faranno aumentare la quantità di calcoli necessari per raggiungere il minimo.
Gradiente di una funzione
Quanto abbiamo scritto sopra ci ha rinfrescato il concetto di derivata di una funzione ad una variabile utile per risolvere una regressione lineare semplice. Ma nel caso di una regressione lineare multipla con più features come dobbiamo procedere?
Il procedimento è analogo, sarà necessario andare a calcolare le derivate parziali di ogni feature per poi ottenere un gradiente che non è altro che il vettore di tutte le derivate parziali calcolate.
Graficamente in un grafico a tre dimensioni come nell’esempio qui sotto la derivata parziale della funzione f rispetto al piano alla variabile x sarà data dall’inclinazione della retta t1 mentre rispetto alla seconda variabile y sarà data dall’inclinazione della retta t2.

